Vi afrunder lige uge 8 med dette indlæg om pentagoner og polyeder.
Vi starter med det sidste.
Polyeder er 3-dimensionelle, rummelige figurer, hvis sider er polygoner. Der findes mange polyeder, men de regulære ser sådan ud
Tetraeder
Et regulært tetraeder består af fire ligesidede trekanter. Navnet er dannet ud fra det græske ord tetra, som betyder fire.
Hexaeder
Et regulært hexaeder, som er det samme som en terning, er et polyeder med 6 sider, som alle er kvadrater. Navnet er dannet ud fra det græske ord hexa, som betyder seks.
Oktaeder
Et regulært oktaeder består af otte ligesidede trekanter. Navnet er dannet ud fra det græske ord okta, som betyder otte.
Dodekaeder
Et regulært dodekaeder består af tolv regulære femkanter. Navnet er dannet ud fra det græske ord dodeka, som betyder tolv.
Ikosaeder
Et regulært ikosaeder består af tyve ligesidede trekanter. Navnet er dannet ud fra det græske ord ikosi, som betyder tyve.
Andre eksempler]
I vor omverden findes utallige eksempler på polyedre, som ikke er platoniske polyedre.
En pyramide er et polyeder med ligebenede trekanter som sider og en grundflade, som typisk er kvadratisk. Den er den form, vi tænker på, når vi forestiller os en ægyptisk pyramide.
En diamant er slebet, så hele overfladen udgøres af plane flader (facetter). Den er et eksempel på en genstand med form som et polyeder.
Den Sorte Diamant er en bygning udformet som et polyeder sammensat af firkanter, som ikke er regulære.
Fælles for alle disse polyeder er, at denne sætning gælder for dem alle:
Eulers polyedersætning, (efter L. Euler), matematisk sætning, som siger, at hvis h, k og f er henholdsvis antallet af hjørner, kanter og sideflader i overfladen af et konvekst polyeder, da gælder altid, at h−k+f = 2.
Du kan se de forskellige polyeder her:
Som før på denne blog, vil jeg vise jer, hvordan man kan konstruere en regulær polygon helt uden brug af vinkelmåler
Denne gang bliver det en pentagon (femkant)
Jeg har lavet en lille billedserie, og hvis i følger den, skulle i meget gerne ende op med en regulær pentagon.
Start med at tegne en cirkel
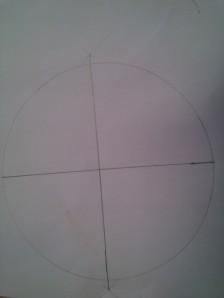Indtegn først cirklens diameter og dernæst en midtnormal til diameteren (Linjestykkerne er tegnet korrekt – det er bare billedet der snyder)
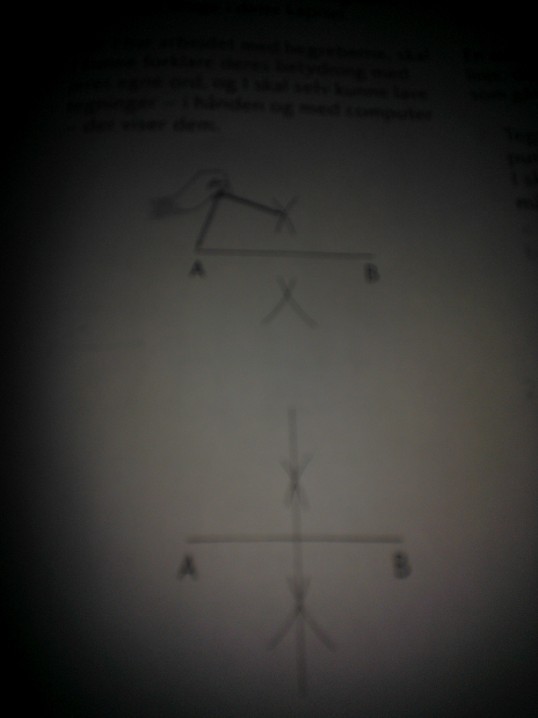
Sørg for at afstanden mellem din passernål og passerens blystykke er lig cirklens radius. Sæt nu passernålen på et af de punkter, hvor en linje skærer cirkelperiferien. Tegn en halvcirkel. De steder, hvor halvcirklen skærer cirkelperiferien, forbindes med en streg som vist på billedet. Derudover indtegner du punkt a og b som vist. (Der hvor den linje, du lige har trukket, skærer den vandrette linje i cirklen kalder du punkt a. B-punkten er hvor den lodrette linje rammer cirkelperiferien for oven)
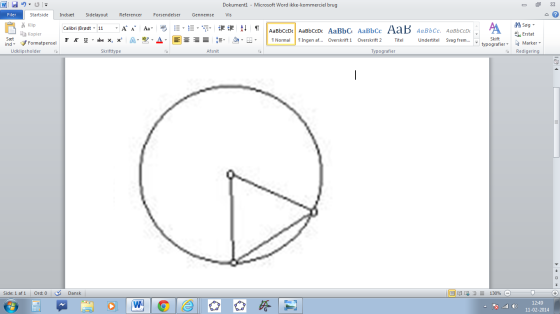
Først sørger du for, at afstanden mellem din passernål og passerens blystykke er lig afstanden mellem punkt a og b. Placer passernålen i punkt af og blystykket i punkt b. Tegn linjen til den rammer den lodrette linje i cirklen. Det punkt kalder du c. Afstanden fra punkt b til c skal nu også være afstanden mellem din passernål og passerens blystykke. Sæt passernålen på punkt b og tegn en de to punkter på cirkelperiferien, som passeren kan nå. Sæt nu passernålen på det ene af de to punkter du har lavet (der hvor din lille streg skærer cirkelperiferien) og tegn det næste punkt. Gør det samme ved det nye punkt. Nu har du 5 punkter, som hvis du forbinder dem, udgør en regulær pentagon. TILLYKKE!
Er der spørgsmål? – Fyr bare løs
Das Bielether
bielether 